Oefening 3: de weg naar Rome

Doel

Statische methoden implementeren, testen en visualiseren.

Opdracht

1. Maak en test methodes voor Caesar's code.
2. Maak en test methodes voor verschillende meetkundige bewerkingen.

Encryptie

1. Een eenvoudige manier om een tekst te encrypteren is gekend als Caesar's code. Elke letter in de tekst wordt een vast aantal posities geroteerd. Bvb. met een rotatie over 1 positie: A in de tekst wordt versleuteld B, B wordt C, etc. Z wordt A. Voor de eenvoud beschouwen wij enkel hoofdletters. Alle karakters krijgen een waarde zoals bepaald door de Unicode standaard. Het is mogelijk om met karakters te rekenen, omdat achter de schermen deze waarden worden veranderd. Let op, in de Unicode tabel wordt met hexadecimale getallen gerekend.

   1. Maak een klasse Caesar.
   2. Maak een statische methode genaamd rotRechts die een Caesar's code uitvoert op een tekst. De tekst invoer is de eerste parameter van de methode, het aantal posities om te roteren is de tweede parameter. De terugkeerwaarde is de geëncrypteerde tekst.
   3. Het is mogelijk een karakter uit een String te halen door de methode charAt(pos) aan te roepen op de String. Het eerste character begint op index 0. bvb.

      String tekst = "abc";
      char a = tekst.charAt(0);
      char b = tekst.charAt(1);
      char c = tekst.charAt(2);
      

   4. Als je een int bij een char optelt dan wordt dit een int. Om dit opnieuw naar een char te converteren moet je een cast uitvoeren. Dit doe je door het gewenste type tussen haakjes voor de te casten waarde te plaatsen. bvb.

      String tekst = "Dit is: ";
      System.out.println(tekst + ('a' + 1));
      System.out.println(tekst + (char)('a' + 1));
      

      Vraag 1

      Bij een rotatie rechts van 13 posities wat is de geëncrypteerde tekst voor "DITISEENHELELANGEZINDITKANJEBETERDOOREENCOMPUTERLATENENCRYPTEREN"?
      

   5. Maak een statische methode in de Caesar klasse genaamd rotLinks die ook een rotatie maakt, maar dan de andere richting uit.

      Vraag 2

      Wat is het aantal posities waarover de volgende geëncrypteerde tekst werd verschoven?
      "JKFKMKNKOSZKQYZOYBKKRZKKKTBUAJOMZKGINZKXNGRKT"
      

2. Maak een methode encrypteer die de te encrypteren tekst als parameter vraagt en als terugkeerwaarde de geëncrypteerde tekst teruggeeft. De tekst wordt woord per woord geëncrypteerd. De eerste letter van elk woord wordt 1 positie naar rechts geroteerd.De tweede 2 posities, etc. Een zin mag bestaan uit hoofdletters en spaties. Spaties worden niet geroteerd.

Vraag 3

  Wat is de gedecrypteerde tekst?
  "EGCI HGKINSAMTCE JU WGHP UG FGQZTAKQP UG BEKXJXOIUOY WKQH KG OKHX"

Meetkunde

1. Veel wiskundige bewerkingen vind je terug in de Math klasse.Bvb. om gebruik te maken van de waarde pi:

   double straal = 1;
   double oppervlakteCirkel = straal * straal * Math.PI;
   

   of om de sinus te berekenen (in radialen):

   double sinus = Math.sin(Math.PI / 2);
   

2. Maak een methode berekenOppRegelmatigeVeelhoekom de oppervlakte van een regelmatige veelhoek te berekenen aan de hand van het aantal zijden en lengte van deze zijden. De oppervlakte van een regelmatige veelhoek kan berekend worden met de volgende formule:

   

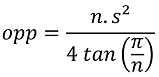
   Hierbij staat n voor het aantal zijden en s voor de lengte van 1 van die zijden.

   Vraag 4

    Wat is de oppervlakte van een regelmatige achthoek met als lengte van de zijden 32m? (Antwoord uitgedrukt in vierkante meter)
   

3. De orthodromische afstand is de kortste afstand tussen twee punten op de oppervlakte van een sfeer. Stel r is de straal van de sfeer, x1,y1 en x2,y2 zijn de coördinaten op deze sfeer. Dan wordt de orthodromische afstand uitgedrukt als:

   

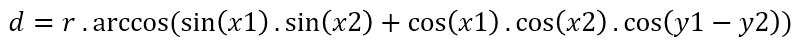
   Maak een methode berekenOrthodromisch om de orthodromische afstand te berekenen. Bereken de afstand tussen jouw woonplaats en Rio de Janeiro. De gemiddelde straal van de aarde is 6371,01 km. Maak gebruik van negatieve getallen om zuid en oost coördinaten voor te stellen. Noord en west zijn dan positief.

4. De afstand tussen twee punten, aangeduid met hun coördinaten, kan berekend worden aan de hand van de stelling van Pythagoras. Maak een methode berekenLengte die rekening houdt met de verschillende mogelijke situaties: y1 = y2, x1 = x2, x1 > x2, etc.

   

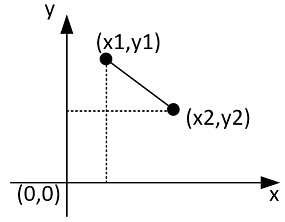
5. Maak twee methodes om een punt te bepalen aan de hand van zijn poolcoördinaten. De ene methode poolNaarCartesischX geeft de x cartesische coördinaat terug en de andere methode poolNaarCartesischY geeft de y cartesische coördinaat terug.

6. Test alle methoden aan de hand van MeetkundeTest.java, deze testen zijn terug te vinden op Toledo.

7. Op Toledo staat een klasse GUI. Importeer deze klasse. Roep de methode teken aan, met de x,y coördinaten van drie punten A, B en C. bvb.

   GUI.teken(45,45, 25, -25, 75, -75);
   

   Probeer deze punten op de cirkel te tekenen. De straal van de cirkel is 175, de oorsprong ligt in (0,0). Tip: gebruik hiervoor de methodes poolNaarCartesisch.