Hoofdstuk 2: Algoritmes

Algoritmes

Software, zoals je misschien al weet van de vorige hoofdstukken, leveren de instructies aan de computerhardware. Zonder software kan de computer niet werken. De CPU zou blijven wachten tot hij een instructie krijgt. Soms is software reeds aanwezig in de hardware (zoals CPUs of in ROM geheugen). In deze gevallen zijn de instructies ingebakken_of _hard-coded in de chip.

Een digitaal uurwerk is een voorbeeld van zo'n hard-coded software. Misschien heb je er nooit bij stilgestaan, maar er is software nodig om de cijfers op het scherm te laten verschijnen. De hardware zorgt ervoor dat de software kan werken.

In dit hoofdstuk leggen we uit wat programma's zijn en hoe ze werken.

Computerprogramma's

Wat is een computerprogramma?

Een computerprogramma is een set van instructies of opdracht, die we code noemen en die door de CPU wordt uitgevoerd. Programma's of software bestaan in vele vormen. Deze kunnen opgedeeld worden in 3 categorie\"en: besturingssystemen, hulpprogramma's en toepassingen.

Een programma of software bestaat in feite niet uit 1 bestand maar uit meerdere bestanden. Elk bestand bestaat uit een naam en een extensie, gescheiden door een punt (bv. Word.exe Voor Windows gebaseerde systemen (tot nu toe het meest gebruikte besturingssysteem) worden deze programma's onderscheiden door hun extensie.

• Uitvoerbare bestanden (.exe, .com) Een uitvoerbaarbestand in een Windows-besturingssysteem is een deel van een programma dat de instructies naar de CPU stuurt. De inhoud van het programma wordt in het geheugen geladen en de CPU zal stap voor stap de instructies uitvoeren die in het geheugen zitten gecodeerd.

• Dynamic Link Libraries (.dll) is een deel van het programma dat algoritmes bevat dat door een uitvoerbaar bestand kan gebruikt worden. Een dergelijk bestand is een ``bibliotheek'' met algoritmes die wanneer het programma deze nodig heeft, kan gebruiken. Bovendien kunnen ook deze bestanden ook gedeeld worden met andere programma's.

• Initialisatie bestanden (.ini) bevatten configuraties, zoals de grootte van een het venster, de kleur van de achtergrond. Deze informatie helpt het programma opstarten (waar moet het verschijnen, werkt de gebruiker liever met een donkere of heldere achtergrond).

Hardware/Software Interactie

Software is de reden waarom computers verkocht worden. Zonder software ben je met een computer niet veel. De instructies in een programma worden uitgevoerd door de CPU en moeten dus in de code geschreven zijn dat de CPU begrijpt. Dit is de reeds genoemde microcode of machinecode.

De microcode is een soort code. De code zijn de stappen (letterlijk de lijntjes code in een programma). Het hangt er vanaf in welke taal het computerprogramma is geschreven. Is het programma geschreven in microcode, dan kan de CPU die uitvoeren. Maar programmeren in microcode is extreem moeilijk en zeer tijdrovend. Vroeger deed men dit aan de hand van ponskaarten. Fouten in de code opsporen was enorm moeilijk.

Andere computertalen maken het leven van programmeurs gemakkelijk. Deze bevatten een taal die (relatief) begrijpbaar is, zodat men sneller kan programmeren. Computertalen vergemakkelijken het maken van programma's. Programmeren is strikt, het moet precies aan de grammatica en aan de spelregels van de taal voldoen. Als we praten of schrijven maken we fouten, maar toch kunnen we elkaar begrijpen. Spellingsfouten of fouten tegen de grammatica in een computertaal zullen het programma verhinderen van correct te verlopen. Deze syntaxfouten moeten dus vermeden worden. Vroeger was dit een heel tijdrovende job (niet zo tijdrovend als het schrijven en verbeteren van microcode). Tegenwoordig zijn de programma's waarin we programma's kunnen maken slim genoeg dat ze fouten kunnen detecteren en zelf kunnen corrigeren.

Programmeren is ook zeer spannend. Eerste en vooral krijg je als programmeur de kans om iets nieuws te cre\"eeren. Hiervoor moet de programmeur soms al zijn creativiteit gebruiken. Elk probleem kent zijn uitdaging en het is aan de programmeur om oplossingen te voorzien. Soms bestaan er meerdere oplossingen tot een probleem.

Machinecode

In Hoofdstuk 2 hebben we gezien dat de computers gebruik maken van het binair getallenstelsel. Geheugens kunnen enkel 0 en 1 beweren. Opdrachten voor de CPU zijn gecodeerd in een specifiek opeenvolging van nullen en enen. Deze code noemt men ook de machine code.

Programmeren in de machinecode is perfect mogelijk maar heel moeilijk. Programmeertalen maken het makkelijker om te programmeren. Deze talen gebruiken een set van woorden die wij als programmeur kunnen begrijpen. Het opgemaakte code is vervat in een {\em bronbestand} en noemen we de {\bf broncode}. De meest gebruikte programmeertalen zijn C, C++ en Java.

Wanneer je een stuk programma gemaakt hebt in een bepaalde programmeertaal, moet dit vertaald worden naar machinecode. de CPU kan enkel machinecode begrijpen. Dit kan op twee manieren: compileren of interpreteren.

Compileren vertaalt alle broncode naar machinecode en resulteert in een uitvoerbaar bestand (bv: .exe). De uitkomst van het compilatieprocess is de objectcode. De programmeur kan de objectcode kopiëren naar een systeem met gelijkaardige eigenschappen als de computer waar het programma gemaakt is (zelfde CPU, zelfde moederbord, zelfde besturingssysteem) en het uitvoerbaar bestand daar uitvoeren. Compileren wordt gedaan met behulp van een {compiler}. Voor java is die javac. Veel grafische omgevingen voor programma's te maken doen dit al vanzelf, zodat je met een enkele druk op de complitieknop een bestand kan compileren. Compileren zorgt ervoor dat alle programma's reeds vertaald is en is dus sneller. Het resultaat is een "stand-alone" versie van je programma, dat op elke (gelijkaardige) computer kan uitgevoerd worden. Hoewel een wijziging van de code (hoe klein ook) zorgt ervoor dat het programma telkens moet hercompileerd worden. Voor kleine programma's is dit geen probleem, maar voor grote programma's kan dit compilatieproces lang duren. De populaire internetbrowser Firefox duurt ongeveer 6 uur om te compileren.

Interpreteren vertaalt ook broncode naar machinecode, maar in tegenstelling tot compileren gebeurt dit lijn per lijn en wordt ook lijn per lijn uitgevoerd. Er wordt dus geen objectcode gemaakt. De lijn wordt als het ware ``on thŽ fly'' vertaald en uitgevoerd. Hierdoor wordt elke wijziging ook direct meegenomen in de vertaling. Het nadeel is dat elke lijn (hoeveel je het programma ook uitvoert) wordt vertaald en dat gaat gepaard met snelheidsverlies. Bovendien moet de broncode altijd doorgegeven worden, willen andere mensen je programma ook gebruiken.

Documentatie

Een heel belangrijk deel van een programma, misschien wel het belangrijkste is de documentatie van een programma. Naast een handleiding van het programma, kan de programmeur in de broncode ook commentaar schrijven. Op deze manier kan een andere programmeur die ook aan de broncode moet werken of moet verder bouwen aan de code begrijpen wat de eerste programmeur bedoeld.

Nagenoeg elke programmeer taal bevat de mogelijkheid om commentaar te schrijven bij elke code. Bijvoorbeeld in de programmeertalen Java en C worden commentaren aangegeven . Al hetgeen tussen deze tekens staan wordt als commentaar beschouwt. Dit betekent dat het compiler deze lijnen zal overslaan. Hierdoor kunnen we commentaar in het programma schrijven.

Hieronder vind je een voorbeeld van een stuk broncode, voorafgegaan met een commentaar. Het stuk commentaar legt uit wat het programma (in dit geval het tonen van de tekst "Hello World!") doet. Later zie je een andere manier van het geven van commentaar via het teken \verb+//+ wordt de rest van de lijn als commentaar beschouwd.

''' /**

• The HelloWorldApp class implements an application that
• simply displays "Hello World!" to the standard output. */ class HelloWorldApp { public static void main(String[] args) {

   System.out.println("Hello World!"); //Display the string.
  

  } } '''

Goede documentatie kunnen we verkrijgen door o.a. :

• Het gebruik van betekenisvolle namen.
• Het goed aangeven van verschillende delen van het algoritme (deelproblemen) met hun juiste functie.
• Het voorzien van gepaste commentaar die juist en verhelderend is en niet alleen herhaalt wat duidelijk uit de instructies van het programma af te lezen valt.
• Een duidelijke schikking gebruiken.
• Documentatie bij het programma voegen met:
  • de volledige beschrijving van de opgave of het probleem
  • enkele voorbeelden van uitvoering
  • een handleiding die beschrijft hoe het programma moet worden gebruikt
  • eventueel een organigram om bepaalde programmadelen nader te verklaren

Algoritmen en flowcharts

Algoritmen: een definitie

Een voorbeeld van een algoritme kan je vinden in de middelste kolom van het IVU diagram (zie tabel \ref{tab:IVU}). Algoritmen zijn exacte beschrijvingen van acties voor de oplossing van verschillende problemen. In de loop van dit jaar zullen we meerdere algoritmen tegenkomen, zelf opstellen en bespreken tijdens het oplossen van problemen. Om een algoritme voor te stellen bestaan er verschillende modellen. Hiervan bespreken we enkel de flowchart. Het is een grafische notatievorm die op een eenduidige wijze de werking van een algoritme beschrijft. Het gebruik van een dergelijke notatievorm is onontbeerlijk om elke verwarring te vermijden. \vspace{1em}

Een algoritme is een geordende reeks ondubbelzinnige, uitvoerbare stappen die een proces beschrijven.

De definitie schrijft voor dat de stappen in een algoritme geordend moet zijn. Dat betekent dat de stappen in een algoritme een zorgvuldig opgebouwde structuur moeten hebben als het gaat om de volgorde waarin de stappen uitgevoerd moeten worden. Dat betekent echter niet dat de stappen in een vooraf vastgelegde volgorde uitgevoerd moeten worden. Parallelle algoritmen, bijvoorbeeld, bevatten een reeks stappen die door meerder processors kunnen uitgevoerd worden terzelfdertijd.

De definitie schrijft ook voor dat de stappen uitvoerbaar moeten zijn. Neem de instructie: `Maak een lijst van positieve gehele getallen''. Dit is een onmogelijke opgave omdat er oneindig veel gehele getallen zijn. Computerwetenschappers (programmeur en informatici) gebruiken de term {\em effectief} om het concept dat stappen uitvoerbaar moeten zijn te benoemen. Een stap is effectief als diedoenbaar' is.

Aan wat moet een algoritme voldoen:

• De basisstappen worden gebruikt om de oplossing voor een gegeven probleem voor te stellen in de vorm van instructies.
• Een algoritme neemt invoerwaarden en produceert een uitvoer
• Na het produceren van een resultaat, moet het algoritme be\"eindigd worden
• Het moet geschreven worden in een begrijpbare taal al dan niet gepaard met eenvoudige wiskundige uitdrukkingen

De eigenschappen van een algoritme zijn:

• Er mogen geen dubbelzinnige instructies (of basisstappen) in het algoritme zitten. b.v. "tel er 10 bij op".
• Er mogen geen onzekerheden inzitten over de instructies die moeten uitgevoerd worden in de volgende stap.
• De instructie moet eenvoudig zijn. Bij een te complexe instructie, moet deze opgesplitst worden in meerdere instructies.
• Er moet een eindig aantal instructies of basisstappen genomen worden gegeven de invoer tot de gewenste uitvoer.
• Het algoritme moet altijd de correcte uitvoer produceren. Bij het nogmaals doorlopen van het algoritme moet altijd dezelfde uitvoer geproduceerd worden.
• Eens de uitvoer geleverd is, wordt het algoritme afgelopen.

Voorbeelden van een Algoritme

In het dagelijks leven komen we veel voorbeelden tegen van handelingsvoorschriften. Enkele voorbeelden zijn:

• een recept: dit beschrijft stapsgewijs hoe je een gerecht bereidt.
• een breipatroon of een weefpatroon.
• een muziekpartitituur: dit is in zoverre bijzonder dat het resultaat de uitvoering zelf is: als die afgelopen is, is er alleen de herinnering.
• een choreografie voor een dansvoorstelling
• een methode voor het optellen van twee getallen, zoals onderwezen in het basisonderwijs

In sommige van deze gevallen dit geval kan er enige vrijheid zijn in de interpretatie van het voorschrift, of wordt het nodige aan de fantasie van de uitvoerder overgelaten; in het geval van een recept is die soms expliciet aangegeven als bijvoorbeeld “zout en peper naar smaak toevoegen”. Door deze interpretatievrijheid kan een uitvoering van het voorschrift wel eens mislukken; maar in het geval van recepten en muziekpartituren levert dat ook de broodnodige variatie in resultaten op.

In andere gevallen is er geen ruimte voor interpretatie en eigen fantasie: het algoritme schrijft precies voor wat de stappen zijn, waarbij elke stap precies gedefinieerd is. Dit soort algoritmen lenen zich voor automatisering. Ook in het geval van het bereiden van een gerecht is is dit soms mogelijk – een broodbakmachine is daarvan een voorbeeld. Een typisch voorbeeld is het algoritme voor het optellen van twee getallen in decimale representatie, zoals dit in het basisonderwijs onderwezen wordt: hier is geen eigen inbreng of fantasie nodig, en het opvolgen van de stappen leidt gegarandeerd tot het juiste resultaat. Als we in de informatica spreken over algoritmen, veronderstellen we dat een automatische uitvoering mogelijk is.

Basisstructuren voor het maken van algoritmen

De opbouw van een algoritme is te verwezenlijken door drie basisstructuren:

• sequentie van meerdere acties
• selectie uit een aantal acties
• herhaling van acties.

Daar elke actie op zijn beurt weer een sequentie, selectie of herhaling kan zijn, kan men zo alle ingewikkelde structuren ontwerpen voor algoritmen. Zo kan bijvoorbeeld de actie binnen een herhaling bestaan uit een selectie. In andere woorden; we herhalen meerdere keren een selectie die telkens 1 actie uit meerdere acties uitvoert. Het zal later duidelijk worden hoe we de verschillende basisstructuren in elkaar gebruiken om complexere algoritmes samen te stellen.

De sequentie

Bij deze basisstructuur volgen de stappen (acties of opdrachten) elkaar op en indien ze allen na elkaar uitgevoerd werden op een correcte wijze bekomt men na de laatste stap ook de oplossing van het probleem of deelprobleem.

• stap 1
• stap 2
• stap 3

De selectie

Hier wordt een keuze gemaakt uit een of meerdere opdrachten afhankelijk van een bepaalde waarde. Deze voorwaarde kan een logische ofwel een rekenkundige uitdrukking zijn die een bepaalde waarde vertegenwoordigt, en afhankelijk hiervan zal deze of een andere opdrachten worden uitgevoerd.

Voorbeelden van selecties zijn:

• als ik dorst heb dan ga ik een glas water drinken.
• als ik de lotto win dan koop ik die wagen anders moet ik mij tevreden stellen met de fiets.

Deze basisstructuur maakt het mogelijk dat een programma afhankelijk van een zeker tussenresultaat een beslissing neemt hoe de loop van het programma verder gaat. Dit betekent dat een computer zelfstandig beslissingen kan nemen.

De Herhaling

Een aantal opdrachten of acties worden geen, een of meerdere keren uitgevoerd om een bepaald doel te bereiken. Hoe dikwijls de herhaling gebeurt wordt weer bepaald door een voorwaarde. We kunnen de volgende mogelijkheden onderscheiden:

• We weten vooraf hoeveel keren het moet gebeuren, dan kunnen we een telling doorvoeren. We kunnen met andere woorden bijhouden hoeveel keer de reeks stappen in de herhaling is gebeurt.
• We weten vooraf niet hoeveel keren het moet gebeuren maar we kunnen zeggen dat als dit verschijnsel zich voordoet we moeten stoppen met het herhalen van de opdracht(en).

Hier zijn twee gebruikelijke structuren mogelijk:

• zolang de voorwaarde waar is voeren we de opdrachten uit en is de voorwaarde niet meer waar dan gaan we verder met de volgende opdracht.
• herhaal de opdrachten totdat de voorwaarde waar is

Het onderscheid tussen beide is dat in de 'zolang'-structuur de voorwaarde eerst gecontroleerd wordt, waar bij de 'herhaal'-structuur eerst de opdrachten uitgevoerd worden en daarna pas de voorwaarde gecontroleerd wordt. De voorwaarde wordt dus bij elke herhaling gecontroleerd.

Flowcharts

Er bestaan meerdere modellen om een algoritme voor te stellen. Het meest gebruikte is zeker onze taal. Maar daar de begrippen en woorden zeer uitgebreid zijn en er zelfs woorden en constructies bestaan met verschillende betekenissen, is het in vele omstandigheden heel nadelig enkel de taal als hulpmiddel te gebruiken.

In bepaalde gevallen zal de omgeving van het probleem bepalend zijn welk model gekozen wordt. Van deze modellen vereist men wel dat ze een gestructureerde en modulaire opbouw mogelijk maken.

Wij gebruiken flowcharts om een algoritme op te stellen. Er worden symbolen gebruikt die volledig aangepast is aan het gestructureerd programmeren. Voor elke basisstructuur is er een symbool. Deze symbolen worden verbonden door pijlen, zodat men de ÒflowÓ van het algoritme kan volgen in het diagramma.

Een flowchart is een diagramma dat een algoritme voorstelt. Elke stap in het proces wordt voorgesteld door een symbool en bevat een korte beschrijving van de uit te voeren stappen. Typisch toont een flowchart de stroom van de gegevens in een algoritme, de operaties of stappen die op de gegevens moeten uitgevoerd worden. Het beschrijft welke operaties moeten uitgevoerd worden om een gegeven probleem op te lossen.

Een flowchart kan je vergelijken met een blauwdruk of een plan van een gebouw. Een ontwerper maakt een plan van een gebouw, vooraleer aan te vatten met de eigenlijke constructie ervan. Op een gelijkaardige manier zal een programmeur eerst een plan maken van zijn programma. Flowcharts kunnen hierbij gebruikt worden.

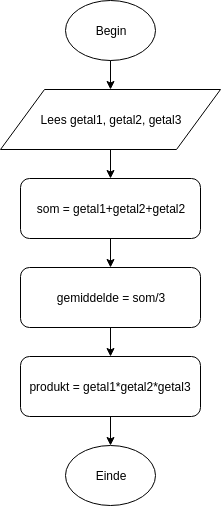
Bijvoorbeeld, stel dat we som, gemiddelde en het produkt moeten berekenen van 3 getallen die door de gebruiker (wij) moeten ingevoerd worden. Een algoritme hiervoor zou kunnen zijn in eenvoudige mensentaal:

• Algoritme som_gemiddelde_produkt:
  • Lees getal1, getal2, getal3
  • Bereken som = getal1 + getal2 + getal3
  • Bereken gemiddelde = som/3
  • Bereken produkt = getal1 getal2 getal3

Hierbij stelt * de vermenigvuldig voor. Een flowchart voor het bovenstaande algoritme kan er als volgt uitzien.

Voordelen van flowcharts

• Communicatie: Flowcharts zijn een goede manier om de logica van een algoritme te communiceren naar andere personen
• Effectieve analyse: Via een flowchart kan het probleem op een goede manier geanalyseerd worden (hoe snel zal het programma lopen, hoeveel instructies zullen er zijn,...)
• Documentatie: Het programmeren van flowcharts kan dienen als een goede documentatie
• Efficient coderen: Flowcharts kunnen dienen als een leidraad om een programma te maken en de code te schrijven
• Efficient opsporen van fouten: Via een flowchart kunnen we stap voor stap het programma overlopen en kunnen we gemakkelijker weten waar er fouten optreden en hoe we deze kunnen oplossen.
• Efficient onderhoud van programma's: We kunnen veel efficiënter het programma onderhouden zodat we elementen kunnen toevoegen over verwijderen.

Beperkingen van flowcharts

• Complexe logica: In sommige gevallen kan de logica van een probleem (en dus ook het programma) heel complex zijn, zodat de flowchart ook heel complex wordt
• Veranderingen: Veranderingen aan een flowchart kan resulteren in het feit dat de volledige flowchart moet hertekend worden.

Wanneer een flowchart gebruiken

Het beste is om een flowchart op te stellen wanneer je een nieuw project begint en wanneer je een probleem moet oplossen door het programmeren van een programma. Een flowchart helpt je een plan op te stellen hoe je het probleem moet oplossen. Ookal is dit een ruwe schets van het uiteindelijke programma, het helpt je gedachten te ordenen en een takenlijst op te stellen. In die zin deel je het probleem op in kleine deelproblemen die elk afzonderlijk moeten opgelost worden.

Flowcharts worden ook gebruikt als communicatie tijdens overleg met teamleden. Via deze flowcharts kunnen discussies gevoerd worden over hoe het probleem het best wordt aangepakt. Daarnaast zijn flowcharts heel handig om als documentatie te gebruiken om een process of een gegevensverloop te schetsen.

Flowchart symbolen

Flowcharts kunnen we op vele manieren opmaken. Meestal worden ze opgebouwd uit een aantal gestandaardizeerde symbolen. Sommige symbolen worden heel frequent gebruikt. We zullen een flowchart altijd starten met een begin en een eind.

Begin- en eindpunt

Het volgende symbool duidt meestal op een begin- en eindpunt van een programma.

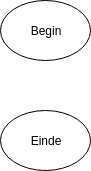
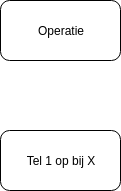
Instructie of Operatie

Een rechthoekig symbool duidt aan dat er een operatie of een instructie moet uitgevoerd worden. Dit kan onder de vorm van tekst of wiskunde zijn: "Tel 1 op bij X" of "som = getal1 + getal2". Als we meerdere acties willen voorstellen, dan tekenen we meerdere symbolen.

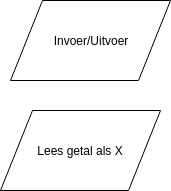
Invoer of Uitvoer

Een blok in de vorm van een parallellogram stelt meestal invoer of uitvoer van gegevens voor. Bijvoorbeeld: "Lees gegevens in van toetsenbord", "Toon waarde van som",...

Selectie

Bij deze basisstructuur wordt een actie uitgevoerd afhankelijk van een te controleren voorwaarde. Bij de eerste vorm is de voorwaarde een logische uitdrukking. Dit is een uitdrukking die waar of niet waar is.

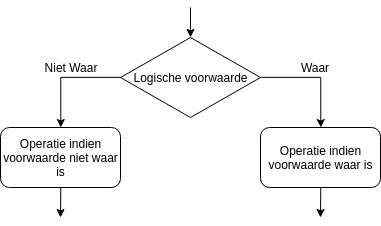
Bij deze basisstructuur horen twee acties. Slechts een van de twee acties wordt uitgevoerd afhankelijk van de voorwaarde. Als het antwoord op de voorwaarde ja is,wordt de ja-actie uitgevoerd, anders de nee-actie.

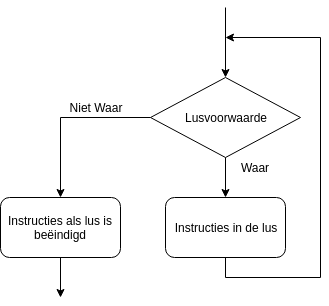
Herhaling

Bij deze structuur wordt een actie herhaald zolang een voorwaarde waar blijft. Op deze manier blijft de code als het ware in een lus. Dergelijke structuren worden ook wel lussen genoemd. Bij elke herhaling van een lus wordt een een aantal instructies herhaald. Deze instructies kunnen ook op hun beurt andere basisblokken bevatten (operaties, selecties, invoer/uitvoer of herhalingen). In feite kan je de code lezen, zolang de lusvoorwaarde waar is worden de instructies (of basisblokken) in de lus herhaald, indien niet dan wordt de lus verbroken.

Flowchart symbolen met de blokken omgeving

In de oefeningenlessen zullen we blokken gebruiken om flowcharts te maken. Dit is een visuele programmeeromgeving waarbij we heel eenvoudige programma's kunnen maken. De bedoeling is om algoritmische zaken onder de knie te krijgen. We gaan een overzicht geven van de traditionele symbolen in een flowchart en de symbolen die in blokken wordt gebruikt. Voor meer informatie omtrent de omgeving blokken verwijzen we naar de oefeningenlessen.

Instructie en operatie

Een voorbeeld van een selectie vind je hieronder. het is een verzameling van 8 instructies: de 4 eerste instructies initializeren de variabelen tekst, resultaat, som en som_tekst. Initializeren betekent hetzelfde als een waarde toekennen aan het begin van een programma of stuk code (methode). Hierdoor weet de computer welke waarde een variabele heeft en kan hij daarmee verder werken. Indien we dit niet doen, bv bij de variabele tekst dan zouden moeten we iets weergeven terwijl de computer niet weet wat hij moet weergeven.

Het bovenstaande doet het volgende:

• Stel de variabele tekst in op "Welkom bij blokken!"
• Stel de variabele resultaat in op de waarde 16
• Stel som in op 5 + 4 (dus 9)
• Stel som_tekst in op "" (een leeg stuk tekst)
• Toon de waarde van tekst op het scherm
• Voeg aan het einde van som_tekst toe: "De som van 5 en 4 is "
• Voeg aan het einde van som_tekst toe, de waarde van som
• Toon de waarde van som_tekst op het scherm

Invoer en uitvoer

In het vorige voorbeeld zat reeds iets met uitvoer: een stuk tekst op het scherm tonen. Hieronder vind je ook een voorbeeld om iets op te vragen via invoer van een gebruiker.

De bovenstaande flowchart gaat:

• De variabele leeftijd instellen op een waarde die de gebruiker moet ingeven. Daarbij krijgt hij de boodschap "Geef je leeftijd in!"
• De waarde van leeftijd tonene op het scherm

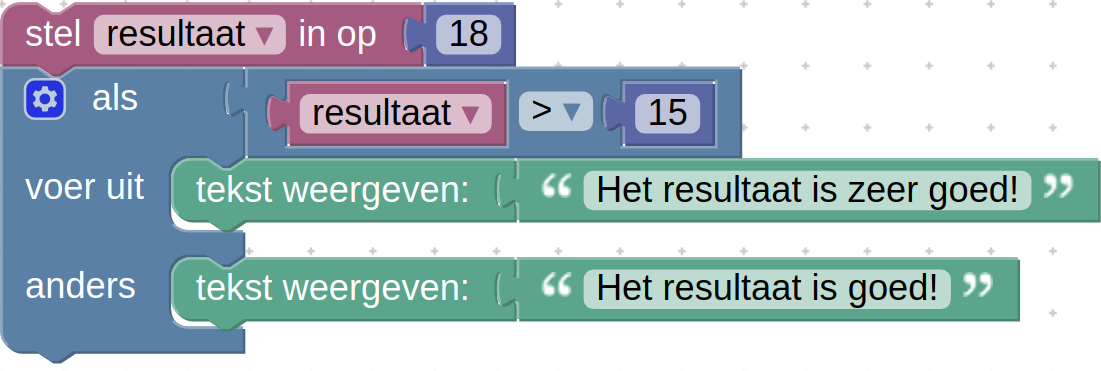
Selectie

Een voorbeeld van een selectie in blokken is:

Lussen

Een voorbeelde van een lus is:

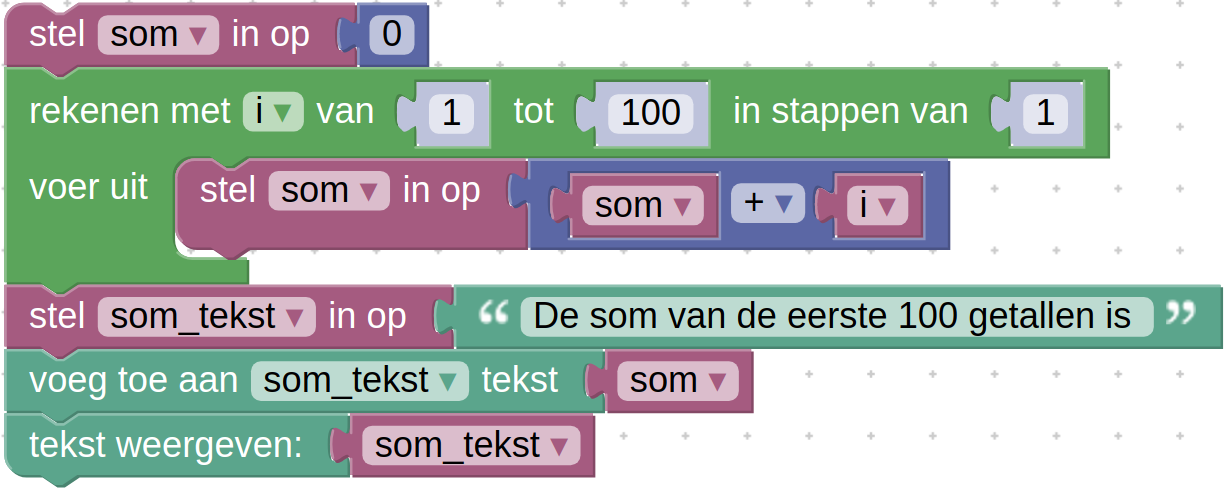
Bovenstaande flowchart berekent de som van de eerste 100 getallen. Dit gaat als volgt:

• Initializeer som op nul (ken de waarde 0 toe aan variabele som)
• reken met i van 1 tot 100 in stappen van 1
  • stel som in aan de huidige waarde van de som met de waarde van i
• Stel de variabele som_tekst in op "De som van de eerste 100 getallen is "
• Voeg aan som_tekst de waarde van som toe aan het einde
• Geef de waarde van som_tekst weer

Oefeningen

1. Maak een flowchart in blokken dat drie getallen inleest en dat de grootste van de drie getallen weergeeft.
2. Maak een flowchart in blokken dat de re\"ele wortels van een vierkantsvergelijking toont. Als er geen re\"ele wortels zijn moet er op het getoond worden dat de wortels imaginair zijn.
3. Maak een flowchart in blokken dat een getal inleest, de faculteit van een getal berekent en het resultaat weergeeft.
4. Maak een flowchart in blokken dat de grootste van de n elementen weergeeft.
5. Aan de Westvlaomse skoale worden in een bepaald vak scores toegekend op basis van de 3 punten: T1, T2 en T3. Als de som van de punten groter is dan 225, moet er op het scherm de letter "G" worden weergegeven (van geslaagd), anders de letter "N". Bovendien is het zo dat als het cijfer T1 kleiner is dan 90, de student sowieso niet geslaagd is (er moet dus een "N" op het scherm komen) ongeacht de waarde van T2 en T3.