Hoofdstuk 8: Methodes

Inleiding

Methodes kunnen gebruikt worden om herbruikbare code de definiëren en om programmeren te vereenvoudigen

• Stel dat je de som moet berekenen van de getallen 1 tot 10, 20 tot 37 en 35 tot 49. Een stuk code die dit doe zou er als volgt kunnen uitzien:

• Je ziet heel veel herhalingen en veel kopieer-en-plak waarbij enkel getallen veranderd zijn. Je merkt dat de drie herhalingen een structuur hebben die je kan bevatten in een algemene methode. Het enige wat je dient te doen is een functie maken en de nodige getallen meegeven aan de functie. Dergelijke functies zullen we methodes noemen die parameters nodig hebben een retourwaarde teruggeven.
• Het bovenstaande stuk code kunnen we herschrijven als volgt:

• Een methode is verzameling van uitdrukkingen die een operatie uitvoeren.

Definiëren van een methode

Een methode definitie bestaat uit een naam van de methode, parameters, type van de retourwaarde en een body

• De syntax voor een methode is als volgt:

• Neem als voorbeeld een methode die het maximum bepaald uit 2 gehele getallen (int). De naam van de methode is logischerwijs max en het aantal parameters die de methode nodig heeft is 2, nl. 2 gehele getallen num1 en num2. De methode bepaald het maximum en geeft een resultaat. Dit resultaat wordt opgeslaan in de retourwaarde en die is ook van het type int. Als modifier gebruiken we public static in dit ganse hoofdstuk. In een latere cursus zullen we dit veranderen.

Definitie van een methode

aanroepen van een methode

• De methode bestaat uit twee delen: een header en de body van de methode. De header specifieert de modifiers, type van de retourwaarde, naam van de methode en parameters.
• Een methode kan een waarde genereren, hiervoor dient Java te weten welk type de methode kan geven. We noemen dit ook wel retourneren, van het Engels return a value.
• De variabelen die gedefinieerd worden in de header noemen we ook formele parameters of eenvoudigweg parameters. Een parameter is zoals een plaatshouder: wanneer een methode aangeroepen wordt, dan geven we een waarde door voor deze parameters. Deze waarde noemen we ook wel de actuele parameters of argument. De lijst van parameters duidt aan op het type, volgorde en aantal parameters van de methode.
• De naam van de methode en de lijst van de parameters (met hun type en de volgorde) noemen we de signatuur van een methode. Parameters zijn optioneel, dat wil zeggen dat een methode kan geen parameters bevatten. Een voorbeeld van een dergelijke methode is Math.random(), deze methode genereert willekeurig getal tussen 0 en 1 en heeft geen parameter nodig.
• De body van de method bevat een verzameling van uitdrukkingen dat de methode implementeren. Het is belangrijk dat als de methode een waarde terug moet geven er een return-uitdrukking is met het sleutelwoord return.

Aanroepen van een methode

Een methode-aanroep voert de code uit die gedefinieerd is in de methode

• In een methode definitie, defineer je wat de methode moet doen. Om de methode effectief uit te voeren, moet je de methoden aanroepen.
• Het programma dat de methode aanroept noemen we de aanroeper of in het Engels caller. Er zijn twee manieren om een methode aan te roepen, afhankelijk indien de methode een waarde teruggeeft of niet.
• Als een methode een waarde teruggeeft, dan wordt de aanroe.p van de methode behandeld als een waarde:

• Bovenstaande uitdrukking roept de methode max aan waarbij de formele parameters worden ingevuld met de actuele parameters 3 en 4 en kent het resultaat van de methode toe aan de variabele groter.
• Wanneer het type van de retourwaarde gelijk is aan void dan geeft de methode geen waarde terug, dan wordt de aanroep behandeld als een uitdrukking. Bijvoorbeeld, de methode println geeft niets terug (maar toont iets op het scherm).

• Wanneer een programma een methode aanroept, dan wordt de controle van het programma getransfereerd naar de aangeroepen methode. Aan aangeroepen methode geeft de controle terug aan de aanroeper wanneer het return-uitdrukking wordt uitgevoerd of wanneer de eindigende accolade is bereikt.

void versus Waarde-retournerende methodes

Een void methode geeft geen waarde terug

• Dit is een voorbeeld van een void methode:

• De methode printGraad is een void methode omdat de methode geen waarde terug geeft. De methode toont iets op het scherm afhankelijk van de parameter punten.
• Om het verschil te zien tussen een void methode en een waarde-retournerende methode kunnen we bovenstaande codefragment herschrijven zodat de methode printGraad omgevormd wordt tot berekenGraad.

Parameter doorgeven: pass by value

Parameters worden doorgegeven als waarde wanneer de methode aangeroepen wordt

• De kracht van het gebruik van methodes ligt hem in het feit dat we parameters kunnen gebruiken. Wanneer het programma een methode aanroept dan moet je actuele parameters meegeven in dezelfde volgorde als de formele parameters in de signatuur van de methode. Dit is ook gekend als parameter volgorde associatie.
• Bijvoorbeeld, onderstaand programma toont een boodschap op het scherm n keer:

• Je kan nPrintln("Hallo", 3) gebruiken om 3 keer de boodschap Hallo op het scherm te tonen. De aanroep nPrintln("Hallo", 3) geeft de actuele string parameter Hallo door aan de parameter boodschap en geeft de waarde 3 door aan de parameter aantalkeer. De uitdrukking nPrintln(3, "Hallo") zal fouten geven, want Java wil het eerste parameter associeren met de eerste formele parameter boodschap, maar die types zijn niet verenigbaar.
• Let op De actuele parameters geassocieerd zijn met de formele parameters in volgorde, aantal en compatibel type.
• Wanneer je een methode aanroept met een argument, dan wordt de waarde van het argument doorgegeven aan de parameter van de methode. Dit wordt pass-by-value genoemd. Als het argument een variabele is en geen letterlijke waarde (literal value), dan wordt de waarde van die variabele doorgegeven aan de methode. De variabele zelf wordt niet aangepast. Een voorbeeld:

geeft:

Voor de aanroep x is 1
De waarde van n in de methode is 2
Na de aanroep x is 1

Modularizatie van code

Modularizatie maakt code gemakkelijker om te onderhouden, om fouten te detecteren en maakt het mogelijk om stukken code te hergebruiken

• Methodes kunnen gebruikt worden om overtollige (of redundante) code te verminderen en laten toe om codefragementen te hergebruiken. Methodes kunnen ook gebruikt worden om code te modularizeren en de kwaliteit te verbeteren van het programma.
• Om een voorbeeld te geven: priemgetallen zijn getallen die enkel deelbaar zijn door 1 en door zichzelf. Hun toepassing ligt heel veel binnen cryptografie en versleuteling van gegevens. Maar het bepalen van priemgetallen is niet eenvoudig. Voor cryptografie willen we een zo groot mogelijk priemgetal vinden, maar hoe groter een getal wordt hoe meer kans dat het delers heeft. Het zoeken van een priemgetal is een probleem waarvan je niet zomaar kan het 100000ste priemgetal kan opvragen. ER is geen formule die dit berekend. Er moet getal per getal gekeken worden indien het een priemgetal is of niet. In dit geval kunnen we het probleem "zoek het n-de priemgetal" onderverdelen in twee problemen: "bepaal indien het getal een priemgetal is" en "print het getal".

Overladen van methodes

Overladen van methodes laat ons toe om methodes te definieren met dezelfde naam, zolang hun signatuur verschillend is

• In sommige gevallen wil je een methode schrijven waarvan je wil dat er verschillende types argumenten kunnen meegegeven worden. Bijvoorbeeld, je kan de methode max schrijven die het maximum bepaalt van 2 gehele getallen. Maar die getallen kunnen als argument meegegeven worden als het type int maar ook als type double voor kommagetallen.
• Zodoende heb je twee methodes met dezelfde naam:

• Als de methode max aangeroepen wordt en je geeft als parameter 2 gehele getallen van het type int mee, dan weet Java dat hij de eerste methode moet gebruiken. Idem, als er twee kommagetallen meegegeven (type double) worden, dan wordt de tweede methode aangeroepen.
• Dit staat bekend als overlade van methodes: dit is het gebruik van methodes met dezelfde naam, maar waarvan de signatuur verschillend is. De Java compiler bepaalt welke methode die hij moet gebruiken op basis van de signatuur.
• De signatuur van de methode wordt bepaald door het type van de parameters en de volgorde van de parameters.

Bereik van variabele

Het bereik van een variabele is het deel van het programma waar de variable kan opgevraagd worden.

• Een variabele gedefinieerd binnen een methode wordt gerefereerd als een lokale variabele. Een lokale variabele moet gedeclareerd en geïnitializeerd (er moet een waarde aan toegekend zijn) vooralleer het gebruikt mag worden.
• Een parameter van een methode is eigenlijk een lokale variabele, en het bereik van een parameter beperkt zich tot de methode. Een variabele gedeclareerd in de initializatie deel van een for-lus heeft een bereik gelijk aan de ganse lus. Een variabel gedeclareerd in de for-lus heeft een bereik dat strekt van het begin van de declaratie tot het einde van de for-lus. Bijvoorbeeld:

Abstracties van methodes en stapsgewijze verfijning

De sleutel tot software ontwikkeling is het toepassen van het concept van abstractie

• Abstracties van methodes worden bereikt doordat het gebruik van de methode los staat van zijn informatie. Een programmeur kan een methode gebruiken zonder dat hij hoeft te weten hoe de methode geïmplementeerd is. De details van de implementatie zitten verborgen in de methode en verborgen van de programmeur in een "black box". Een voorbeeld hiervan is de methode System.out.println, deze methode toont een stuk tekst op het scherm, maar de details van de implementatie weten we niet (en hoeven we ook niet te weten).
• Het bovenstaande concept kan geburikt worden in het process voor het ontwikkelen van progamma's. Bij het schrijven van programma's kan je de strategie van verdeel-en-heers toepassen, ook wel bekend als stapsgewijze verfijning. Deze strategie bestaat erin om een probleem onder te verdelen in subproblemen. Deze subproblemen kunnen op hun beurt verder opgedeeld worden in kleinere, meer bevattelijke problemen.

Top-Down ontwerp

• Beginnende programmeurs gaan vaak de oplossing in detail uitwerken vanaf de start als ze aan het probleem werken. Hoewel, detail in het finale programma zeker van belang is, kan deze manier van werken het probleemoplossend denken in de weg staan.
• In een Top-Down ontwerp starten we van het grote probleem en gaan we het probleem opdelen in deelproblemen.
• Eens we niet meer verder kunnen dan kunnen we van de deelproblemen methodes maken. We geven hierbij een gepaste naam en gepaste signatuur. Daarna implementeren we de methode. Je kan de methode zien als een taak, die het deelprobleem moet oplossen.

Voordelen van stapsgewijze verfijning

• Stapsgewijze verfijning deelt een groot probleem op in kleinere overzichtelijke deelproblemen. Elk deelprobleem kan geïmplementeerd worden via een methode. Deze benadering maakt het programma gemakkelijker om te schrijven, te hergebruiken, te testen en te veranderen.

Het programma wordt eenvoudiger

• In plaats van een lange reeks uitdrukkingen te schrijven, wordt de code opgedeeld in methodes en aanroepen naar die methodes. Dit vereenvoudigt het programma en maakt de code beter leesbaar en verstaanbaar.

Methodes kunnen hergebruikt worden

• Soms kunnen deelproblemen ook voorkomen in andere problemen. Het genereren van willekeurige getallen komt zowel voor bij een lotto-spel als bij het gooien van een dobbelsteen. Door gebruik te maken van stapgewijze verfijning kunnen we die methodes ook hergebruiken in andere stukken code.
• Voorlopig kunnen we dit doen via knippen en plakken van een methode, maar later zullen we zien dat we deze methode ook in een klasse kunnen plaatsen en dat we die klasse kunnen importeren in ons programma. Dit is gelijkaardig aan hoe we de klasse Scanner importeren, die het ons een verzameling van tools geeft om tekst of getallen te kunnen ingeven.

Ontwikkeling, testen en debuggen van code wordt gemakkelijker

• Aangezien elk deelprobleem opgelost kan worden via een methode, kunnen we elk van die methodes individueel gaan testen en debuggen als er een fout in zit. Het gemakkelijker om de fout (zowel syntax als semantische fouten) te isoleren en op te lossen.
• Bovendien moeten we niet het ganse programma in een keer oplossen. We kunnen beginnen met een soort skelet van het programma en vullen daarna de gaten in. Een beetje zoals je een boek/thesis begint met eerst de titels en ondertitels te schrijven. Hierdoor weet je welke tekst je op welke plaats moet schrijven.
• In het begin lijkt alsof het opdelen van een programma in methodes meer tijd kost, vooral omdat je alles moet uitdenken en de opdeling maken in methodes. Maar uiteindelijk spaart het veel tijd in de eindfase van de ontwikkeling omdat je makkelijker kunt fouten vinden, deze isoleren en oplossen.

Teamwerk wordt eenvoudiger

Wanneer een groot programma opgedeeld wordt in methodes, kan de implementatie van deze methodes gedelegeerd worden over een team van programmeurs. Elke persoon is verantwoordelijk voor het schrijven van zijn stukje code.

Toepassing: Recursie

Inleiding

Recursie is een techniek als alternatief voor complexe lusstructuren

• Stel dat je een in een map in verkenner alles bestanden wil vinden die een specifiek woord bevatten. Hoe kan je dit probleem oplossen? Hoe kan je ook in submappen kijken? Je moet dus recursief gaan kijken ook in de submappen.
• In deze toepassing gaan we even in op recursieve methodes. Dergelijke methodes roepen zichzelf op en dit is een nuttige programmeertechniek.

Gevalstudie: Berekenen van faculteit

• Veel wiskundige functies kunnen gedefinieerd worden met recursie. Een eenvoudig voorbeeld is het berekenen van de faculteit van een getal n als volgt:

$\begin{array}{lc} 0! = 1; & n = 0\\ n! = n \times (n - 1)!; & n > 0 \end{array}$

• Hoe vind je n! voor geen gegeven n? Om 1! vinden is het makkelijk want 0! = 1 en $1! = 1 \times 0!$. Veronderstal dat je weet wat $(n-1)!$ is dan kan je direct $n!$ berekenen door $n! = n \times (n-1)!$.
• Laat de methode faculteit(n) een methode zijn dat $n!$. Als je de methode uitvoert met n = 0 dan kan het resultaat onmiddellijk gegeven worden. De methode weet dus hoe het het meest eenvoudige geval moet oplossen. Dit noemt soms wel het basisgeval of het stopcriterium.
• Als n != 0 dan kan je de faculteit berekenen door $n \times faculteit(n-1)$.
• Het recursieve algoritme voor de faculteit berekenen kunnen we beschrijven als:

• Een aanroep van een recursieve methode kan resulteren in veel aanroepen van diezelfde functie, want de methode zal het probleem blijven onderverdelen in deelproblemen totdat het het basisgeval tegenkomt. Om een recursieve methode te beëindigen, moet het probleem gereduceerd tot het basisgeval of stopcriterium. De aangeroepen functie zal de berekening uitvoeren en het resultaat teruggeven aan de methode die de functie heeft aangeroepen.
• Een volledige java-programma om de faculteit te berekenen zie je hieronder:

• Een grafische voorstelling van het uitvoeren van een recursieve functie vind je hieronder. De figuur toont wat er gebeurt als we faculteit(4) uitvoeren.

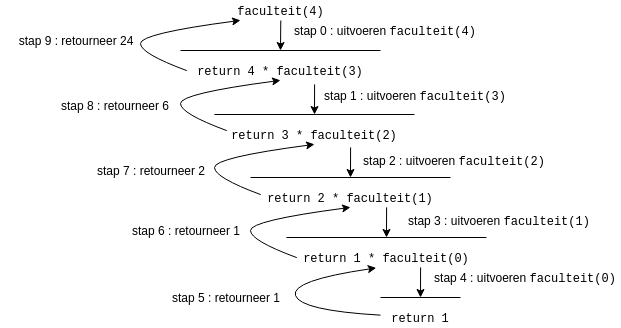
• Opgelet
  • De berekening van een faculteit kan in de werkelijkheid beter en efficiënter berekend worden met een lus. We hebben dit gebruikt om het concept recursie uit te leggen.
  • Bij recursie moet er immers ervoor gezorgd worden dat het probleem reduceert tot het basisgeval. Indien dit niet gebeurt kan dit aanleiding geven tot oneindige recursie. Bijvoorbeeld het volgende stukje code zal aanleiding geven tot dit:
    public static int faculteit(int n){ return n * faculteit(n - 1); }
    

Gevalsstudie: Berekenen van Fibonacci getallen

Problemen oplossen met recursie

• De voorgaande voorbeelden zijn twee klassieke voorbeelden van recursie. Alle recursieve methodes hebben de volgende eigenschappen:

  • De methode wordt geïmplementeerd gebruik makende van een if-else of switch uitdrukking dat verschillende gevallen definieerd
  • één of meerdere basisgevallen moeten gebruikt worden om de recursie te beëindigen
  • Elke recursieve aanroep reduceert het oorspronkelijk probleem dichter bij het basisgeval.

• In het algemeen, zal recursie het probleem onderverdelen in deelproblemen, die hetzelfde is als het oorspronkelijk probleem maar dat kleiner is. Recursie is overal en het is leuk om recursief te denken. Veronderstel het tonen van een boodschap op het scherm n keer. Je kan dit onderverdelen in 2 subproblemen:

  • Het ene deelprobleem is om de boodschap één keer op het scherm te tonen
  • het andere deelprobleem bestaat erin om de boodschap n-1 te tonen
• Het tweede probleem is hetzelfde als het oorspronkelijke maar kleiner in grootte. Het basisgeval voor het probleem is n == 0. Een implementatie van dit systeem kan je zien als:

Gevalsstudie: Torens van Hanoi

• Eerder werd er verteld dat problemen die opgelost worden met recursie, eigenlijk ook opgelost kunnen worden met een lus of een selectie. Er zijn ook problemen die heel moeilijk op te lossen zijn via een lus, maar die eenvoudig op te lossen zijn met recursie. Een voorbeeld van een dergelijke probleem is "De torens van Hanoi".